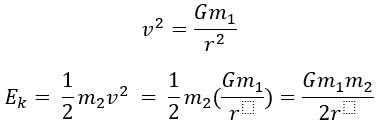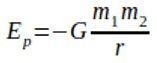– The concept of escape velocity ?esc=√2???

• Escape Velocity: The initial velocity required by a projectile to rise vertically and just escape the gravitational field of a planet.
• During the rise experienced when travelling at an escape velocity, the projectile’s kinetic energy transforms into gravitational potential energy such that:

Ek (initially) = Ep (finally)

• By considering the kinetic and gravitational energies of a projectile, it can be shown mathematically that the escape velocity of a planet depends only upon the universal gravitational constant, the mass of the planet, and the radius of the planet:

kinetic energy loss :  ,   where v_i  = initial velocity

potential energy gain :  , where r is the radius of the earth

Escape velocity =

• The escape velocity does not depend upon any intrinsic property of the projectile.
• The escape velocity of Earth works out to be approximately 40 000 km h^-1.

– total potential energy of a planet or satellite in its orbit U=−????

• Gravitational Potential Energy (E_p): The energy of a mass due to its position within a gravitational field.
• As part of the Law of Universal Gravitation, the inverse square law relates the strength of a gravitational field and the distance from the centre of its source.
• Thus the force of gravitational attraction between an object and a planet will only drop to zero when the object is an infinite distance from the planet.
• At infinity (or a very large distance away) is the level of zero potential energy in space.
• Using this law we calculate force and using  to calculate gain in potential energy.
• Thus, in space, gravitational potential energy is defined as the work done to move an object from infinity (or a very large distance away) to a point within a gravitational field.
• It can be shown mathematically that:

          where:

• m₁ = mass of planet (kg).
• m₂ = mass of object (kg).
• r = distance separating masses (m).
• G = universal gravitational constant.

– total energy of a planet or satellite in its orbit U+K=−???2?

• to calculate this we will first calculate Kinetic energy

• potential energy:  

 – energy changes that occur when satellites move between orbits (ACSPH096)

Since Total Energy only depends on radial distance (as mass remains constant), as the orbit changes , the total energy of the satellite changes

Change in energy

To change orbit, rockets are fired which increase or decrease E_k , to accommodate for this energy. As soon as the satellite changes altitude transformation between E_k and E_p occur , as the satellite settles down in its new orbit.