If a planet/satellite or satellite is moving in uniform circular motion around an astronomical object, Then the gravitational force acts as the centripetal force

mass of the satellite or planet moving in uniform circular motion : m

mass of the object around which the planet or the satellite revolves : M

orbital radius : The radius of the circular path = r

gravitational force :

centripetal force :

centripetal acceleration : The acceleration produced due to centripetal force

orbital period : The time taken to complete one orbit = T

orbital velocity: speed with which the satellite or planet revolves ,

Relationship between velocity and mass of the object at center of circular path and orbital radius

Since we know that the gravitational force provides the centripetal force for uniform circular motion

Relationship between orbital period and orbital radius

We also know that :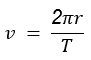

Which means :

Which shows that

Note: This is also known as The third of Kepler’s three laws of planetary motion, which states that the square of the orbital period of a planet is proportional to the cube of its mean distance from the Sun