Kepler’s Laws of Planetary motion

First Law

The orbit of a planet in the solar system is an ellipse, with the Sun at one of the two foci.

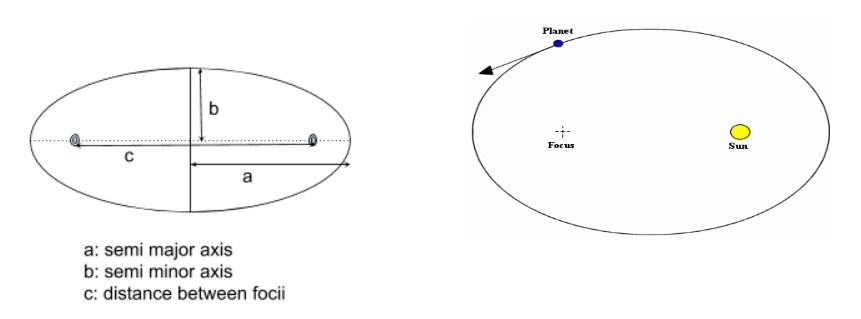
The eccentricity given by determines the flattening of the ellipse

Second Law

A line drawn from the Sun to the planet will sweep out equal areas in equal times.

The three arcs shown in the above picture will take same time to cover, because the area of the sectors within the arcs are same.

since average speed over any arc length is given by , therefore the speed changes in an elliptic path .

The speed in an elliptical orbit is given by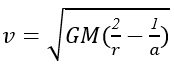

where :

• M = mass of object at focii
• r =radial distance where speed is measured

This implies that Kinetic Energy changes also.

But the total Energy remains constant

Total energy in keplerian orbit =

Third Law

The square of the orbital period of a planet is proportional to the cube of its mean distance from the Sun