Home » EasyPhys » Electromagnetism » Charged Particles, Conductors and Electric and Magnetic Fields » Analyse the interaction between charged particles and uniform magnetic fields
Analyse the interaction between charged particles and uniform magnetic fields
- Magnetic field exert forces on moving charged particles.
- If a particle with charge q is moving with velocity v perpendicularly to a magnetic field with magnetic field strength B, the particle will experience a magnetic force (F), given by : F = qvB
- The direction of such a force is given by the right-hand rule.

- The direction of a is the direction of the velocity of the particle
- The direction of b is the direction of magnetic field B
- The direction of the thumb is the direction of the force experience by the charged particle
- If the velocity is at a certain angle (θ) to the magnetic field, the force is given by:

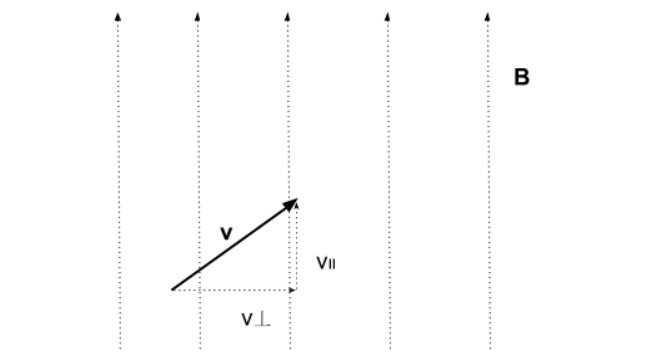
 means that the force acts on only the component of the velocity v which is perpendicular to the magnetic field B , i.e.
means that the force acts on only the component of the velocity v which is perpendicular to the magnetic field B , i.e. 
- In such an instance, the direction of the force is given by using the right-hand rule on the component of the velocity perpendicular to the magnetic field.
Acceleration is given by
- the acceleration is only due to the component of the velocity which is perpendicular to the magnetic field. Hence if particle is moving in the same direction as the magnetic field, no acceleration is produced.
- The acceleration is in the same direction as the force.
- The direction of the acceleration is perpendicular to both velocity v and magnetic field B
Extract from Physics Stage 6 Syllabus © 2017 NSW Education Standards Authority (NESA)
