Electric Field : Electric field is a region around a charged particle or object within which a force would be exerted on any charged particle or object

Electric fields are vector fields.

• At every point the arrow points to the direction in which the field would exert force on a positively charged particle.
• The density of the arrows per unit cross section area gives the strength of the electric field.

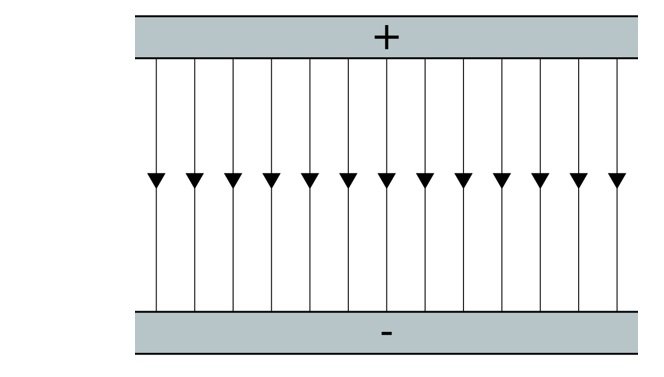
The picture above shows an uniform electric field between two parallely kept charged particles.

At any point in space, an electric field has strength and direction:

• Strength is given by E, in volts per metre (V m^-1).
• Direction is that in which a positive charge will experience a force.

The strength of the Electric field is constant throughout the region in between the electric plates.

• Force on a positively charged particle is
  • where q is the positive charge on the particle
• There for the work done on a particle by this force would be
  • If the charge is moved in a straight vertical line from the negatively charged plate to the positively charged plate then the formula is for work done is simply

• The voltage difference between the two plates is V
• Since Electric field is a conservative field , when the particle is moved from one place to another , the work done gets transferred to mechanical energy.
• mechanical energy gain:
  • 
  • 
  • where q is the charge of the particle
• If a charged particle is moved very slowly from the negatively charged plate to the positively charged plate, then the work done gets converted to gain in potential energy,

Since work done is equivalent to gain in potential energy,

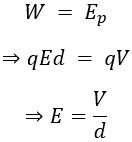
• Therefore the magnitude of the uniform electric field is given by
• Direction is from high to low potential

Relation between charge, mass, acceleration and electric field

• From Newton’s Laws we know that
• In an electric field,
• Equating these, we get