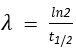The rate of decay of an radioactive isotope is measured by its half life.

Half life : It is the time required for radioactive isotope to reduce to half of its initial value.

• It has been found that the rate at which radioactive isotopes decay , is directly proportional to the number of atoms present. The rate can be expressed as :
  • 
  • (where  is the decay constant , with units s^-1 )
• This equation can be integrated to give the following result :
  • 
  • where,
    • N_o is the number of atoms present at time t = 0
    • N_t is the number of atoms present at time t

• Using the definition of half life , we can find
  • is when the number of atoms are half the original amount, i.e.
  • Thus ,
  • rearranging we get ,
  • Thus if we can measure the half life, we can calculate the decay constant.

Extract from Physics Stage 6 Syllabus © 2017 NSW Education Standards Authority (NESA)