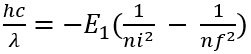To tackle the drawbacks of previous models of atoms such as Rutherford’s, Bohr proposed a modified model of an atom incorporating developments from quantum mechanics in 1913.

The fundamental postulates of his model were as follows:

• The electron is able to revolve in certain stable orbits around the nucleus without radiating any energy contrary to what classical electromagnetism suggests. These stable orbits are called stationary orbits and are attained only at certain discrete distances from the nucleus. The electron cannot have any other orbit in between these discrete ones.
• Electrons can only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency ν determined by the energy difference of the levels according to the Planck relation:
  • h is Planck’s constant
  • is the frequency of the emitted radiation
• The stationary orbits are attained at distances for which the angular momentum of the revolving electron is an integral multiple of the reduced Planck’s constant.
  • angular momentum
    • where reduced Planck’s constant is
  • In these orbits, the electron’s acceleration does not result in radiation and energy loss.

Using the quantised energy levels of the hydrogen atom in his model, and the law of conservation of energy , Bohr was able explain the lines of emission spectrum of hydrogen gas.

The wavelengths of the line emission spectrum was explained as follows:

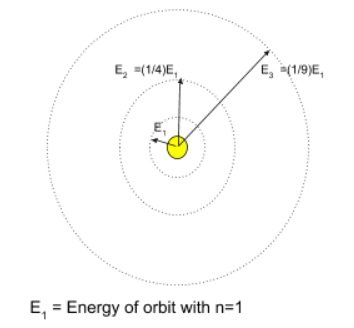
• According to Bohr’s postulates, whenever electrons jump from a stable orbit of higher energy (E₂) to a lower energy (E₁) , it gives out radiation with the frequency v, according to Planck’s relation :
• Thus if we know the energy E₂ and E₁, we will be able to calculate the frequency and wavelength.

Calculation of orbital energies for n^th orbit:

Electrons in a particular orbit have both electrostatic potential energy and kinetic energy.

• Kinetic energy of electron :
  • • m_e=mass of an electron
• • we need to convert this to an expression in terms of charge of electron(q_e) and radius of orbit(r):
  • The electrostatic force between electron and nucleus :
  • q_e= magnitude of the charge on the proton and electron (1.602 x 10^-19 C)
  • This force acts as a centripetal force for the orbiting electron
  • Thus :
  • Thus,
• Potential energy of an electron :
• Total Energy :

According to Bohr’s postulates, electrons can only have restricted angular momentum,  energies and orbits. Let us find out the allowed radius(r) for the electron’s restricted orbits.

• Angular momentum in classical physics :
• Angular momentum of electron allowed by Bohr’s postulates :
  • n is called principal quantum number
• 
• We know v, from the equation :
  • 
• Thus :
• Hence, the radius of the orbit corresponding to principal quantum number – n :
  • radius of the orbit corresponding to principal quantum number – 1 :
  • Combining the gives the relation :

Now we know the radius of allowed orbits , we can calculate the energy in these orbits.

• Total Energy :
• radius of orbit with principal quantum number – n :
  • where :
• Thus Total Energy associated with the orbit with principal quantum number – n:

• Thus if an electron jumped from an orbit with principal quantum number ‘ni’ to another orbit with principal quantum number ‘nf’ . () , Energy released as Electromagnetic radiation would be
• We know . So,
  • 
  • 
  • 
• Applying , and , we get
  • Therefore,

This theoretical derivation gives us the exact form as Rydberg’s modified form of Balmer’s empirical formula!

The value of  , also matches that of Rydberg’s constant!

Extract from Physics Stage 6 Syllabus © 2017 NSW Education Standards Authority (NESA)