Diagram of projectile motion :

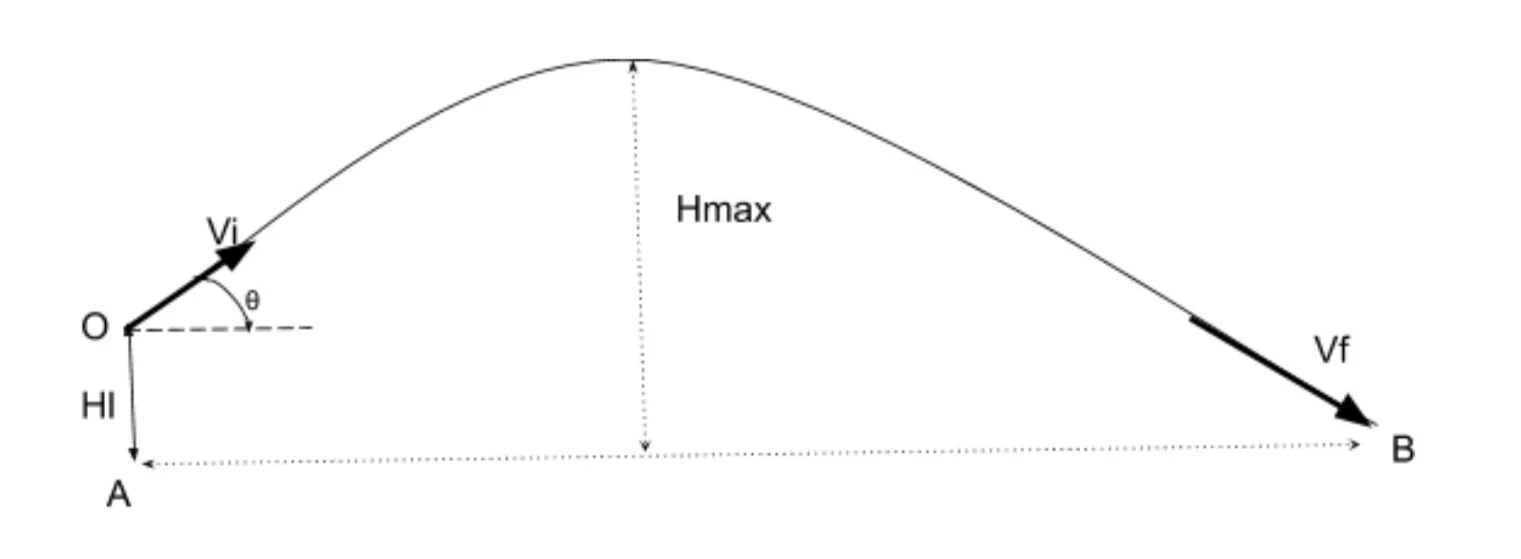
In the diagram :

• Hl : launch height
• Vi : initial velocity
• Vf : final velocity
• θ: launch angle
• H: maximum height
• The distance AB is the ‘horizontal range of the projectile’ .
• The time taken for projectile to travel along the trajectory from O to B is ‘time of flight’

Throughout the motion the vertical movement is affected  by gravitational acceleration  g = 9.8ms^-2

To analyse the quantitative relationships between the variables :

• The vertical and horizontal component of the initial velocity depends on the launch angle
  • Horizontal component : Vi_x = Vi × cos θ
  • Vertical component : Vi_y = Vi × sin θ

• Relationship between max height, launch height, initial velocity and launch angle
  • max height is when vertical component of velocity is zero
  • V_y² = V_y² – 2g(H-Hl) where  is V_y vertical velocity and H is height
  • So when V_y=0, then

• • substituting  Vi_y = V_i × sin θ, max height can be given by

• Relationship between time of flight . initial velocity, angle of launch and launch height
  • time of flight is the time taken for the vertical component of the projectile to reach max height and reach the bottom.
  • using equation :

• • where
  • relation

• • so time :

• Horizontal range of projectile
  • Since the horizontal component of projectile does not experience any acceleration , the horizontal velocity remains constant .
  • So horizontal range is simply Horizontal component of speed X time of flight
  • 
  • 

• Final velocity can be calculated by
  • Energy consideration (Conservation of mechanical energy)
  •