Analyse the experimental evidence gathered about black body radiation, including Wien’s Law related to Planck’s contribution to a changed model of light
- Black Body: A hypothetical object that absorbs all incoming radiation.
- A practical example of an item that resembles a black body is a small hole in a box with a black interior.
- When a black body becomes warmer than its surroundings, it becomes a perfect emitter.
- Black Body Radiation: Electromagnetic radiation that is emitted by a black body.
- The radiation emitted from a black body extends over all wavelengths of the electromagnetic spectrum.
- Classical theory predicted that the intensity of radiation would increase indefinitely as wavelengths
- However, experimental results showed that intensity peaked at a wavelength characteristic of the temperature of the black body.
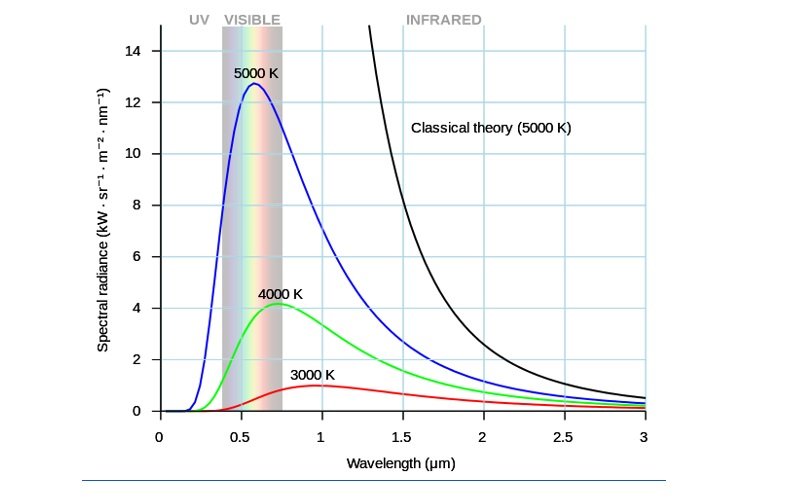
- Moreover, it also showed the wavelength of peak intensity of radiation emitted by a black body decreases as the temperature of the body increases.
- This wavelength of peak intensity
only depends on the temperature of the body. - This relation is defined as Wien’s Law :
, where b = 2.9 x 10-3 Km
- This wavelength of peak intensity
only depends on the temperature of the body.
, where b = 2.9 x 10-3 Km– Plank’s proposal of a new model
- The contradiction between classical theory and experimental results was resolved by Max Planck.
- Planck proposed that radiant energy may be treated statistically as if it were exchanged in multiples of a certain discrete amount, or quanta.
- Each frequency of radiation has a characteristic quantum of energy.
- This is given by the equation: E = hf
- where:
- E = energy in joules (J)
- h = a constant, now known as Planck’s constant (6.63 x 10-34 J s)
- f = frequency in hertz (Hz)
- This assumption allowed Plank to reproduce the results obtained experimentally from theory.
Extract from Physics Stage 6 Syllabus © 2017 NSW Education Standards Authority (NESA)